Eine
Kategorie
ist in der Mathematik ein Gebilde aus sogenannten Objekten und sogenannten Morphismen von einem Objekt zu einem anderen oder zu demselben Objekt.
Morphismen können hintereinandergehängt werden, wenn das Zielobjekt des ersten das Startobjekt des zweiten ist.
Das Ergebnis ist dann ein Morphismus vom Startobjekt des ersten zum Zielobjekt des zweiten.
Außerdem gibt es für jedes Objekt O einen Identitätsmorphismus (im Folgenden notiert mit | oder \ oder /)
von O nach O selbst, der andere Morphismen beim Hintereinanderhängen nicht verändert.
Ich schreibe hier die Hintereinanderhängung von Morphismen durch Untereinanderstellen:
f
g
|
h
ist dasselbe wie
f
g
h
Das steht für einen zusammengesetzten Morphismus von A nach D, wenn wir annehmen dass f von A nach B geht,
g von B nach C und h von C nach D.
Eine bekannte Kategorie ist diejenige Kategorie, in der die Objekte Datentypen sind und die Morphismen Funktionen zwischen diesen Typen. Das Hintereinanderhängen entspricht dabei dem Hintereinanderausführen von Funktionen, und der Identitätsmorphismus ist die Funktion, die ihren Parameter als Ergebnis zurückgibt. Um diese Kategorie soll es im Folgenden hauptsächlich gehen.
Eine andere interessante Kategorie, deren Morphismen keine Funktionen sind, ist die Kategorie, deren Morphismen Relationen zwischen Datentypen sind.
Bei den monoidalen Kategorien kommt noch eine weitere Operation hinzu: Das Nebeneinanderschreiben von Morphismen (und Objekten), genannt monoidales Produkt oder Tensorprodukt. Das monoidale Produkt muss dabei gewisse Bedingungen erfüllen, zum Beispiel:
| | | g f |
f g = | | = | |
| | f | | g
Diese Regeln ergeben sich ganz natürlich aus der benutzten Notation. Das neutrale Element des monoidalen Produkts wird einfach als leerer Raum gezeichnet. Derartige Diagramme nennt man Stringdiagramme.
Es gibt zwei wichtige Möglichkeiten, die Kategorie der Funktionen und Datentypen mit einem monoidalen Produkt auszustatten. Die erste Möglichkeit (die im Folgenden hauptsächlich betrachtet werden wird) ist, das monoidale Produkt von Datentypen als Tupelbildung aufzufassen. Bei zwei einfachen Datentypen T und U ist (T U) dann das kartesische Produkt T×U, und wenn die Faktoren des monoidalen Produkts selbst Tupeltypen sind, ist es die Konkatenation der Tupel, also wird (T×U×V) (W×X) zu (T×U×V×W×X). Das monoidale Produkt von Funktionen ist eine Funktion, die ein Tupel entgegennimmt, es in Teil-Tupel der richtigen Größe zerlegt, diese dann an die Faktorfunktionen weitergibt und deren Ergebnisse wieder zu einem einzigen Tupel zusammensetzt. Man kann dann zum Beispiel Datenflussgraphen wie den folgenden aufschreiben:
|
(3) |
| | (4)
\ / |
+ /
| /
\ /
*
|
Er repräsentiert eine Funktion, die ihr Argument um 3 erhöht und mit 4 multipliziert. Dabei steht (n) für die Funktion, die das leere Tupel auf die Konstante n abbildet.
Bei der anderen Möglichkeit wird das monoidale Produkt von Datentypen T und U aufgefasst als disjunkte Vereinigung T ⊕ U der Datentypen. Ein Element von (T U) ist dann also entweder ein Element von T zusammen mit der Information, dass es zum ersten Faktor gehört, oder ein Element von U mit der Information, dass es zum zweiten Faktor gehört. Das monoidale Produkt von zwei Funktionen ist eine Funktion, die eine von beiden Faktorfunktionen anwendet, je nachdem zu welchem der Faktoren des Input-Typs der Eingabewert gehörte. Ein entsprechendes Diagramm hat dann gewisse semantische Ähnlichkeit mit einem Kontrollflussgraphen. Wie man Schleifen in einen solchen Kontrollflussgraphen einbaut, erzähle ich weiter unten.
Andere interessante monoidale Kategorien: Die Kategorie der Datentypen und Relationen kann man auch relativ einfach mit einem monoidalen Produkt ausstatten. Für die Kategorie der Vektorräume und linearen Abbildungen kann man entweder die direkte Summe oder das Tensorprodukt als monoidales Produkt nehmen. Wenn man das Tensorprodukt nimmt, entsprechen die Stringdiagramme der Penrose-Notation.
Dann gibt es noch die Kategorie der Tangles, deren Objekte natürliche Zahlen und
deren Morphismen Gewirre von Schnüren sind.
Die Zahlen zählen die Schnüre, die sich auf einer bestimmten Höhe befinden.
Eine einfache Schnur, notiert als |, / oder \, ist der Identitätsmorphismus des Objekts 1.
Es gibt zwei elementare Morphismen vom Objekt 2 zu sich selbst: Die Zopfung ,\´ und die inverse Zopfung `/..
Diese stellen zwei sich überkreuzende Schnüre dar. Dann gibt es noch den Morphismus cup
, geschrieben \_/, vom Objekt 2 zum Objekt 0,
und den Morphismus cap
, geschrieben /¯\, vom Objekt 0 zum Objekt 2.
Aus diesen Bausteinen kann man dann durch horizontale und vertikale Komposition beliebige Schnurgewirre zusammensetzen, zum Beispiel:
|
/¯\ /
| `/.
\ / \
,\´ \
/ \ \
/ \ |
/ \ |
| \ /
\ /¯\ `/.
`/. \ / |
/ \ `/. |
/ \_/ | |
| | |
Das ist ein Morphismus von 1 nach 3, weil oben eine Schnur ist und unten drei. Zwei Diagramme bezeichnen denselben Morphismus, wenn sie sich durch Herumbewegen der Schnüre ineinander überführen lassen, wobei der untere und der obere Rand des Diagramms bis auf Abstände der Schnüre unverändert bleiben müssen.
Es ist annäherungsweise möglich, diese Notation in Haskell umzusetzen. In dieser Datei befinden sich die nötigen Definitionen – teilweise allgemein gehalten, aber hauptsächlich für die Kategorie der Datenflussgraphen ausgelegt – und einige Beispiele. Es gibt noch eine ältere, weniger allgemeine aber dafür leichter verständliche Version des Codes.
Da man in Haskell Whitespace nicht als Operator überladen kann und bei der Wahl der Bezeichner für Morphismen auch gewisse Einschränkungen bestehen, musste ich mich folgendermaßen anpassen:
… angegeben.
Ich habe auch damit experimentiert, hierfür Whitespace zu verwenden,
aber die resultierenden Programme können nur wenige Zeilen umfassen, bevor der Typechecker mehrere Gigabyte Speicher anfordert.|> realisiert.
Damit das Layout stimmt, kommt vor dem Operator (fast) immer ein Zeilenumbruch.
+ zum Beispiel zu _plus und | zu
_id. Den neutralen Morphismus, der die Identität
bezüglich der horizontalen Komposition (also des monoidalen Produkts) ist, nenne ich monId.
Konstanten k werden mit (_const k) oder kürzer (mc k) zu
Funktionen gemacht, die das leere Tupel auf das 1-Tupel (k) abbilden.
_dup in Haskell notiert werden.
Wenn ich im Folgenden irgendwo Morphismusschreibe, kann damit auch eine Familie von Morphismen gemeint sein.
(->)), sondern in einen newtype-Typ DataFlow
beziehungsweise ControlFlow verpackt. Ich werde sie im Folgenden trotzdem wie Funktionen behandeln.
Die eingebauten Tupeltypen von Haskell sind für unsere Zwecke nicht verwendbar,
da es keine assoziative Konkatenation von Tupeln gibt und es auch nicht möglich
ist, Funktionen zu schreiben, die Tupel mit beliebig vielen Elementen verarbeiten. Darum wird eigens
eine Typklasse VTup für variadische Tupeltypen
definiert. Sie hat zwei Instanzen, eine für das leere Tupel () und eine zum Hinzufügen eines Elements vorne an das Tupel mit dem Operator
:*:. Um nicht ständig mit diesen Operatoren hantieren zu müssen, gibt es Funktionen um variadische Tupel von und
zu Standard-Tupeln zu konvertieren. Wenn ich
im Folgenden Zwischenergebnisse bei der Auswertung von Datenflüssen angebe, werde ich der Einfachheit halber normale Tupel aufschreiben.
Auch nehmen Haskell-Funktionen normalerweise keine Tupel als Parameter, sondern sind
gecurryt (geschönfinkelt).
Darum kann man nicht einfach gewöhnliche Funktionen als Morphismen für unsere Datenflussgraphen-Kategorie nehmen,
sondern muss gewisse Konvertierungen vornehmen. Haskell-Funktionen, die einen einzigen Parameter und einen Rückgabewert haben,
werden mit der Funktion mf an das variadische Tupel-Format angepasst.
Und die Funktion mc2_1 wandelt eine Haskell-Funktion mit zwei Parametern in einen entsprechenden Morphismus um.
Hier ist ein Beispiel für einen Datenflussgraphen aus Haskell-Quellcode:
test :: Integral a => (a, a)
test = cnCurry $ fromCN . dataFlow
( ( monId )
|> ( (_const 59)… (_const 19) )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… (_const 4)… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( (_swap)… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( _id… (_divMod) )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( (packC)… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( (_swap) )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… (unpack) )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( (_dup)… _id… _id )
|> ( _id… _id… _id… _id )
|> ( _id… _id… _id… (_const _plus)… _id )
|> ( _id… _id… _id… _id… _id )
|> ( _id… _id… _id… _id… _id )
|> ( _id… _id… (_swap)… _id )
|> ( _id… (_del)… _id… _id… _id )
|> ( _id… _id… _id… _id )
|> ( _id… _id… _id… _id )
|> ( _id… _id… _id… _id )
|> ( _id… (apply ) )
|> ( _id… _id )
|> ( _id… _id )
)
Was berechnet er? Um das herauszufinden, schauen wir uns die Morphismen, aus denen er besteht, von oben nach unten an und vollziehen nach,
was mit den Daten passiert, die durch diesen Graphen fließen.
Die erste Zeile ist die Angabe des Haskell-Typs: Integral a => (a, a). Das Endergebnis wird also ein Paar von ganzen Zahlen sein.
Die zweite Zeile enthält Aufrufe der Konvertierungsfunktionen, um das Endergebnis als Haskell-Paar zu erhalten.
Die dritte Zeile ist der eigentliche Beginn der Funktionsdefinition. Diese erste Zeile ist leer; sie enthält nur die monoidale Identität monId.
Die Daten sind also (). Dann werden zwei Konstanten eingeführt:
|> ( (_const 59)… (_const 19) )
|> ( _id… _id )
|> ( _id… _id )
Die Daten sind jetzt (59, 19). Dann wird noch eine Konstante eingeführt:
|> ( _id… _id )
|> ( _id… (_const 4)… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
Die Daten sind jetzt (59, 4, 19). Die ersten beiden Komponenten werden mit der symmetrischen Zopfung (_swap) vertauscht:
|> ( _id… _id… _id )
|> ( (_swap)… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
Die Daten sind jetzt (4, 59, 19). Die Funktion _divMod dividiert
zwei Zahlen und gibt den abgerundeten Quotienten und den Rest zurück:
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( _id… (_divMod) )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
Die Daten sind jetzt (4, 3, 2). Die Funktion packC verpackt die Elemente ihres Argument-Tupels,
so dass sie später mit unpack wieder ausgepackt werden können:
|> ( _id… _id… _id )
|> ( (packC)… _id )
|> ( _id… _id )
|> ( _id… _id )
Genaugenommen verpackt packC die Daten in eine Funktion, die das leere Tupel auf die Daten abbildet.
Daher lassen sich die Daten jetzt in Haskell-Syntax schreiben als ((\() -> (4, 3)), 2).
Anmerkung: Da packC auf beliebig viele Faktoren des Tupels aus der vorherigen Zeile angewendet werden
kann und nicht nur wie hier auf zwei, sollte man nur eine Anwendung von packC pro Zeile haben, damit der Typprüfer es auch versteht.
Die beiden Elemente des Tupels auf der obersten Ebene werden vertauscht und das verpackte Paar wird wieder ausgepackt:
|> ( _id… _id )
|> ( (_swap) )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… (unpack) )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
Die Daten sind jetzt (2, 4, 3). Dann wird das erste Element dupliziert:
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( (_dup…) _id… _id )
|> ( _id… _id… _id… _id )
Die Daten sind jetzt (2, 2, 4, 3). Als nächstes wird die Additionsfunktion in eingepackter Form eingeführt. (_const _plus)
ist dabei ein Morphismus, der das leere Tupel auf das 1-Tupel, das die Additionsfunktion als Element enthält, abbildet:
|> ( _id… _id… _id… (_const _plus)… _id )
|> ( _id… _id… _id… _id… _id )
Die Daten sind jetzt also (2, 2, 4, (\(a, b) -> a+b), 3). Zwei Elemente werden vertauscht und eins gelöscht:
|> ( _id… _id… _id… _id… _id )
|> ( _id… _id… (_swap)… _id )
|> ( _id… (_del)… _id… _id… _id )
|> ( _id… _id… _id… _id )
Die Daten sind jetzt (2, (\(a, b) -> a+b), 4, 3). Die Funktion apply kann nicht nur, wie unpack, konstante
Funktionen vom leeren Tupel auspacken, sondern auch welche mit Parametern. Die Funktion wird dabei angewendet. Die anzuwendende Funktion wird als der
linkeste Input für apply erwartet,
rechts daneben kommen die Argumente:
|> ( _id… _id… _id… _id )
|> ( _id… _id… _id… _id )
|> ( _id… (apply ) )
|> ( _id… _id )
|> ( _id… _id )
Das Endergebnis ist also (2, 7).
Ein Funktor ist eine strukturerhaltende Abbildung zwischen Kategorien (oder innerhalb derselben Kategorie). Das heißt, dass ein Funktor von C nach D Objekte und Morphismen von C auf Objekte und Morphismen von D abbildet, so, dass es unter anderem egal ist, ob man erst zwei Morphismen in C aneinanderhängt und dann das Ergebnis mit dem Funktor zu einem Morphismus von D macht, oder ob man die beiden Morphismen erst mit dem Funktor nach D abbildet und dann die Ergebnisse davon aneinanderhängt.
Ein einfach verständlicher Funktor in der Kategorie der Datenflussgraphen ist der Funktor [] für Listenbildung.
Er bildet jeden Datentyp T auf den Datentyp [T], den Typ aller Listen mit Elementen aus T, ab.
Ein Morphismus f wird auf den Morphismus (map f) abgebildet, eine Funktion, die bekanntlich f auf jedes
Element ihres listenwertigen Arguments anwendet und die Liste der Ergebnisse zurückgibt.
Eine weitere wichtige Art von Funktor ist (T ->), der jeden Datentyp U auf den Typ (T -> U) aller Funktionen
von T nach U
abbildet. Ein Morphismus f wird zu (f .), also einer Funktion höherer Ordnung, die aus ihrem Argument g die Funktion
f . g macht, welche erst g anwendet und dann das Ergebnis nochmal mit f transformiert.
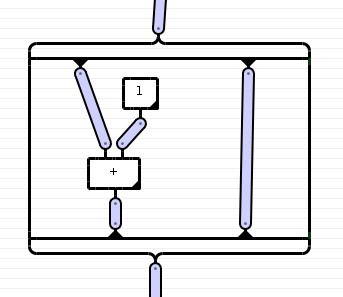
Mit Stringdiagrammen lassen sich auch Funktoren darstellen. Dazu wird um den Teil des Diagramms, der die Morphismen enthält, auf welche der Funktor angewendet wird, ein Rahmen gezogen. So sollte es aussehen:
|
[-------------]
[ | | ]
[ | (1) | ]
[ \ / | ]
[ + | ]
[ | | ]
[-------------]
|
Oder noch graphischer:
Und so sieht es in Haskell aus:
_id
|> _id
|> fd({----}_id…{----------------}_id{---})
|> fd( _id… _id )
|> fd( _id… (_const 1)… _id )
|> fd( _id… _id… _id )
|> fd( (_plus)… _id )
|> fd( _id… _id )
|> fd({-------}_id…{-------------}_id{---})
|> _id
|> _id
Welcher Funktor hier anzuwenden ist, geht aus dem Typ des Identitätsmorphismus in der ersten Zeile hervor.
Hier ist ein Beispiel für den Listenbildungs-Funktor mit einigen zusätzlichen Funktor-Operationen, die ich gleich erkläre:
test2 :: [(Int, [Char])]
test2 = cnCurry $ map fromCN . unsingleton . dataFlow
(
( monId )
|> ( (mc_list [1,2,3]) )
|> ( _id )
|> ( _id… (mc_list "aM") )
|> ( _id… _id )
|> ( fd({-------}_id{--------------------})… _id )
|> ( fd( _id )… _id )
|> ( fd( _id )… _id )
|> ( fd( _dup… (mc 1) )… _id )
|> ( fd( _id… _id… _id )… _id )
|> ( fd( _id… _id… _id )… _id )
|> ( fd( _id… _id… _id )… _id )
|> ( fd( _id… _plus )… _id )
|> ( fd( _id… _id )… _id )
|> ( fd( _id… _id… (mc 2) )<×>_id )
|> ( fd( _mult… _id… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( (mc2_1 div)… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( (mc_list [2,6])… _id… (mf fromEnum) ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… _plus ) )
|> ( fd( _id… (mf toEnum) ) )
|> ( fd( fd({---}_id{-------})… (_id::Typ DF Char) ) )
|> ( fd( fd( _id )… _id ) )
|> ( fd( fd( _id )… _id ) )
|> ( fd( fd( _id )<×>_pure ) )
|> ( fd( fd( _id… (mc 3)… _id ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _plus… _id ) ) )
|> ( fd( fd( _id… _id ) ) )
|> ( join|>fd( _id… _id ) )
|> ( fd( (_id::Typ DF Int)… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _dup… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… (mf fromIntegral)… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… (_id::Typ DF Integer)… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… (mc2_1 genericReplicate) ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd({--------}_id…{------}_id{----------------}) )
|> ( _id )
|> ( _id )
|> ( _id )
)
Wir schauen uns wieder von oben nach unten an, was mit den Daten passiert. Zu Anfang bestehen diese wieder nur aus dem leeren Tupel. Dann wird eine Liste von ganzen Zahlen erzeugt:
( monId )
|> ( (mc_list [1,2,3]) )
|> ( _id )
Die Daten sind jetzt [1, 2, 3]. Es wird noch eine Liste eingeführt, diesmal eine Liste von Unicode-Zeichen:
|> ( _id… (mc_list "aM") )
|> ( _id… _id )
Die Daten sind jetzt ([1,2,3], ['a','M']). Nun öffnen
wir eines der beiden gefunktorten Objekte,
um die Listeneinträge manipulieren zu können:
|> ( fd({-------}_id{--------------------})… _id )
|> ( fd( _id )… _id )
An den Daten verändert das nichts, da ein Funktor, angewendet auf einen Identitätsmorphismus, wieder einen Identitätsmorphismus ergeben muss. Aber wir können jetzt innerhalb der Funktorklammern Funktionen angeben, die auf jedes Listenelement angewendet werden sollen:
|> ( fd( _id )… _id )
|> ( fd( _dup… (mc 1) )… _id )
|> ( fd( _id… _id… _id )… _id )
|> ( fd( _id… _id… _id )… _id )
|> ( fd( _id… _id… _id )… _id )
|> ( fd( _id… _plus )… _id )
Die Daten sind jetzt ([(1,2),(2,3),(3,4)], ['a','M']). Als nächstes werden die beiden Listen miteinander
multipliziert
(Operator <×>).
Dabei wird jedes Element der einen Liste mit jedem Element der anderen Liste zu einem Tupel zusammengefasst. In derselben Zeile wird außerdem
eine 2 in jedes Listenelement eingefügt:
|> ( fd( _id… _id… (mc 2) )<×>_id )
Die Daten sind jetzt [(1,2,2,'a'),(1,2,2,'M'),(2,3,2,'a'),(2,3,2,'M'),(3,4,2,'a'),(3,4,2,'M')].
In der graphischen (nicht-Haskell) Notation würde man hier einfach die Funktor-Rahmen verschmelzen:
[ | | ] | [ | | ] | [ | | ] [---] [ | | (2) ]___[ | ] [ | | | / ] [ | | | / ]
Ein Funktor, mit dem man das machen kann, und der noch ein paar andere Regeln einhält, heißt monoidaler Funktor.
Jetzt kommt ein wenig Arithmetik:
|> ( fd( _mult… _id… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( (mc2_1 div)… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
Die Daten sind jetzt [(1,'a'),(1,'M'),(3,'a'),(3,'M'),(6,'a'),(6,'M')].
Eine Liste wird in jedes Element eingefügt, und für die Zeichen wird der Unicode-Codepoint ermittelt:
|> ( fd( _id… _id ) )
|> ( fd( (mc_list [2,6])… _id… (mf fromEnum) ) )
|> ( fd( _id… _id… _id ) )
Die Daten sind jetzt [([2,6],1,97),([2,6],1,77),([2,6],3,97),([2,6],3,77),([2,6],6,97),([2,6],6,77)].
Das zweite und dritte Element jedes Tupels werden addiert und das Ergebnis soll wieder in ein Zeichen umgewandelt werden.
|> ( fd( _id… _plus ) )
|> ( fd( _id… (mf toEnum) ) )
Allerdings ist die Haskell-Funktion toEnum, die ganze Zahlen in Elemente von Aufzählungstypen konvertiert, zu generisch.
Wir müssen noch angeben, zu welchem Aufzählungstyp, nämlich Char, das Ergebnis gehören soll. Das geht so
(DF ist eine Abkürzung für die Kategorie, DataFlow):
|> ( fd( fd({---}_id{-------})… (_id::Typ DF Char) ) )
|> ( fd( fd( _id )… _id ) )
Die Daten sind jetzt [([2,6],'b'),([2,6],'N'),([2,6],'d'),([2,6],'P'),([2,6],'g'),([2,6],'S'].
Nebenbei wurden noch die Funktorklammern für die innere Liste geöffnet. Als nächstes sollen die Buchstaben mit den Zahlen zu Paaren zusammengefasst werden.
Wenn die Buchstaben in einelementige Listen verpackt wären, könnten wir die Listen wie vorhin multiplizieren, um das zu erreichen.
Der Listen-Funktor ist ein
applikativer Funktor,
daher verfügt er über eine Operation pure
, um Objekte auf kanonische Weise zu gefunktorten Objekten zu machen.
Für Listen ist diese Operation in Haskell gerade das Verpacken in eine einelementige Liste. (Es hätte auch anders sein können.
Eine andere halbwegs sinnvolle Wahl wäre das Erzeugen einer unendlichen Liste mit lauter gleichen Elementen.) Also wenden wir _pure auf
die Buchstaben an und multiplizieren
die [2,6] mit dem Resultat:
|> ( fd( fd( _id )… _id ) )
|> ( fd( fd( _id )<×>_pure ) )
Die Daten sind jetzt [[(2,'b'),(6,'b')],[(2,'N'),(6,'N')],[(2,'d'),(6,'d')],[(2,'P'),(6,'P')],[(2,'g'),(6,'g')],[(2,'S'),(6,'S')]].
Nun wird zu jeder der Zahlen 3 hinzugezählt:
|> ( fd( fd( _id… (mc 3)… _id ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _plus… _id ) ) )
Die Daten sind jetzt [[(5,'b'),(9,'b')],[(5,'N'),(9,'N')],[(5,'d'),(9,'d')],[(5,'P'),(9,'P')],[(5,'g'),(9,'g')],[(5,'S'),(9,'S')]].
Der Listen-Funktor ist eine
Monade.
Das bedeutet, dass er zusätzlich zu den Operationen eines applikativen Funktors eine weitere
Operation besitzt, die join
-Operation: Zwei verschachtelte Anwendungen des Funktors können
auf natürliche Weise transformiert werden zu einer einzelnen Anwendung.
Bei Listen ist diese Operation das Aneinanderhängen der Elemente (die selber Listen sind): Aus einer Liste von Listen wird so eine einfache Liste.
|> ( fd( fd( _id… _id ) ) )
|> ( join|>fd( _id… _id ) )
Die Daten sind nun [(5,'b'),(9,'b'),(5,'N'),(9,'N'),(5,'d'),(9,'d'),(5,'P'),(9,'P'),(5,'g'),(9,'g'),(5,'S'),(9,'S')].
Jetzt werden die Zahlen dupliziert, so dass das erste Duplikat jeweils zu einem Int-Wert wird und die
zweite zu einem Integer-Wert. Warum? Nur so. Um die Interaktion meiner Notation mit dem Typprüfer zu testen.
|> ( fd( (_id::Typ DF Int)… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _dup… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… (mf fromIntegral)… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… (_id::Typ DF Integer)… _id ) )
|> ( fd( _id… _id… _id ) )
Die Daten sind jetzt [(5,5,'b'),(9,9,'b'),(5,5,'N'),(9,9,'N'),(5,5,'d'),(9,9,'d'),(5,5,'P'),(9,9,'P'),(5,5,'g'),(9,9,'g'),(5,5,'S'),(9,9,'S')].
Man sieht hier allerdings keinen Unterschied zwischen Int- und Integer-Werten.
Wir benutzen die zweite Zahl jedes Tripels, um den Buchstaben zu einem String von entsprechend vielen gleichen Buchstaben zu machen:
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… (mc2_1 genericReplicate) ) )
|> ( fd( _id… _id ) )
Das Endergebnis lautet [(5,"bbbbb"),(9,"bbbbbbbbb"),(5,"NNNNN"),(9,"NNNNNNNNN"),(5,"ddddd"),(9,"ddddddddd"),(5,"PPPPP"),(9,"PPPPPPPPP"),(5,"ggggg"),(9,"ggggggggg"),(5,"SSSSS"),(9,"SSSSSSSSS")].
Zum Schluss schließen
wir noch die Funktorbox, um anzuzeigen, dass wir mit dem Manipulieren der Elemente fertig sind:
|> ( fd( _id… _id ) )
|> ( fd({--------}_id…{------}_id{----------------}) )
|> ( _id )
|> ( _id )
|> ( _id )
Wie bereits erwähnt, ist (T ->) ein Funktor, für jeden Parametertyp T.
Wir können dies benutzen, um anonyme Funktionen zu definieren. Hier ist ein Beispiel:
test4 :: Num a => (a, a)
test4 = cnCurry $ fromCN . dataFlow
(monId
|> ( (_const 19) )
|> ( _id )
|> ( _id… (_const _id) )
|> ( _id… fd({---}_id{----------------}) )
|> ( _id… fd( _id ) )
|> ( _id… fd( _id ) )
|> ( _id… fd( _id… (_const 4) ) )
|> ( _id… fd( _id… _id ) )
|> ( _id… fd( _plus ) )
|> ( _id… fd( _id ) )
|> ( _id… fd( _id ) )
|> ( _id… fd({------}_id{-------------}) )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… (_dup) )
|> ( _id… _id… _id… (_const 5) )
|> ( _id… _id… _id… _id )
|> ( _id… _id… (apply) )
|> ( _swap… _id )
|> ( _id… _id… _id )
|> ( _id… _id… _id )
|> ( (apply)… _id )
|> ( _id… _id )
|> ( _id… _id )
)
Mit dem Morphismus (_const _id) wird zunächst eine Identitätsfunktion erzeugt.
Dann werden Funktorklammern geöffnet.
Innerhalb dieser Klammern wird beschrieben, was mit dem Rückgabewert aus der jeweils vorangehenden Zeile passieren soll: Erst
wird der Wert mit der Konstanten 4 zu einem Paar zusammengefasst, dann werden die beiden Elemente des Paares addiert.
Die fertig definierte Funktion ist also die Funktion, die 4 auf ihr Argument addiert.
Diese Funktion wird nun dupliziert und jedes Duplikat wird auf eine Zahl angewendet. Die Anwendung kann man sich so vorstellen, dass
das Argument im linken Rand des Funktorkastens nach oben transportiert wird, am (_const _id) umkehrt und ins Innere des Kastens wechselt,
wo es dann verarbeitet wird. Das Ergebnis wird wieder abwärts transportiert bis zu der Stelle, wo die Funktion angewendet wurde.
Die Vorstellung, dass das Argument versteckt im linken Rand des Funktorkastens nach oben läuft, ist gar nicht mal so abwegig.
Der Funktor (T ->) entsteht nämlich aus dem
Bifunktor
(->) durch Festlegen eines Objekts für das erste Argument des Bifunktors.
Ein Bifunktor ist ein Funktor vom kartesischen Produkt zweier Kategorien in eine Zielkategorie. In unserem Falle ist die zweite
Kategorie sowie die Zielkategorie die Kategorie
der Datenflussgraphen und die erste Kategorie die dazu duale Kategorie, also die Kategorie, bei der alle Morphismen umgedreht sind.
Die Morphismen dieses kartesischen Produkts kann man zum Beispiel so notieren:
f ]+[ g
Mit den Bifunktor-Klammern werden daraus zwei Abteile
:
[ f ]+[ g ]
In Haskell könnte man es so aufschreiben:
f2( f )( g )
Man kann damit folgendes machen:
test12 ::(Num a)=> a -> a
test12 = (unsingleton.)$cnCurry $ dataFlow
( ( _id )
|> ( _id )
|> ( _id )
|> ( (_const _id)… _id )
|> ( f2({----------------}_id )( _id{--------------------})… _id )
|> ( f2( _id )( _id )… _id )
|> ( f2( _id )( _id )… _id )
|> ( f2( _id )( _id… (mc 4) )… _id )
|> ( f2( (Dual _mult) )( _id… _id )… _id )
|> ( f2( _id… _id )( _plus )… _id )
|> ( f2( (Dual(mc 2))… _id )( _id )… _id )
|> ( f2( _id )( _id )… _id )
|> ( f2({------------}_id{---})({------}_id{-------------})… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( (apply) )
|> ( _id )
|> ( _id )
|> ( _id )
)
Hier wird das Argument auf dem Weg nach oben mit 2 multipliziert.
Da das linke Abteil Morphismen der dualen Kategorie enthält, steht das linke Teildiagramm auf dem Kopf.
Für die Morphismen in diesem Abteil ist auch das vertikale Zusammensetzen andersherum definiert.
Um zwei unterschiedliche Bedeutungen der vertikalen Komposition zu haben, muss in Haskell für die Dualen Morphismen
eine newtype-Definition angegeben werden (newtype Dual f=Dual f).
Die Morphismen müssen dann in diesen neuen Typ verpackt werden, entweder indem man immer z.B.
Dual _mult statt _mult schreibt, oder, im
Falle von allgemeinen Kategoriegenerierenden Morphismen wie _id und _swap, als Teil
einer Kategorien-Typklasse.
Die (linke partielle) Spur eines Morphismus lässt sich anschaulich folgendermaßen definieren:
| |
/¯\ | |
| beispielmorphismus
\_/ |
|
Der linkeste Faktor des Zielobjekts wird sozusagen nach oben zurückgeführt und als linkester Faktor des Quellobjekts genommen. Das Nach-oben-Biegen funktioniert aber nur, wenn die Kategorie duale Objekte besitzt, wie zum Beispiel die Kategorie der endlichdimensionalen Vektorräume mit dem Tensorprodukt, bei der die Spurbildung die gewöhnliche Spur eines Tensors berechnet. In der Kategorie der Datenflussgraphen gibt es aber keine dualen Objekte. Ein hypothetisches duales Objekt T* wäre so etwas wie der Typ eines Versprechens, später genau einen Wert vom Typ T zu liefern. Ein solcher dualer Wert müsste vor Verdopplung und Löschung geschützt werden, um sicherzustellen, dass genau ein Wert geliefert wird. Das lässt sich aber nicht erzwingen, wenn sich duale Objekte als vollwertige Objekte der Kategorie verhalten sollen.
Abhilfe können hier Funktoren schaffen, wie ich für die Kategorie der Datenflussgraphen mit dem (T ->)-Funktor demonstriere:
test6 :: Num fr => fr -> fr -> fr
test6 = cnCurry $ unsingleton . dataFlow
(( _id … _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( ({---------}packC{---------}) )
|> ( fd( _id… _id ) )
|> ( param <| fd( _id… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( (_swap)… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… _plus ) )
|> ( fd( _id… _id ) )
|> ( trace |> fd( _id ) )
|> ( fd( _id ) )
|> ( fd( _id ) )
|> ( ({-------}unpack{------------}) )
|> ( _id )
)
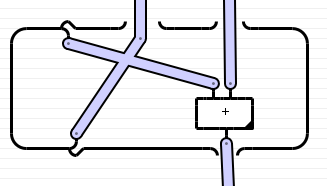
Der Morphismus, dessen Spur gebildet werden soll, hat drei Inputs und zwei Outputs:
( _id… _id… _id )
|> ( (_swap)… _id )
|> ( _id… _id… _id )
|> ( _id… _plus )
|> ( _id… _id )
Die Spur hiervon hat nur zwei Inputs und einen Output. Um die Spur zu berechnen, werden die beiden Inputs zunächst mit
packC in eine nulläre Funktion verpackt.
Dann wird die Funktion param auf das gefunktorte Objekt angewendet.
Die Zeile
|> ( param<| fd( _id… _id ) )
ist eigentlich zwei Zeilen, da <| die vertikale Komposition ist, nur mit vertauschten Parameterrollen.
Aus ästhetischen Gründen habe ich beides in eine Zeile geschrieben.
Die Funktion param transformiert ein Funktionsobjekt so, dass links ein Parameter hinzugefügt wird.
Hier wird also aus einer Funktion vom Typ ()->(a, b) eine Funktion vom Typ (p)->(p, a, b).
Nun kann der Morphismus angewendet werden, dessen Spur wir bekommen wollen. Danach wird die Funktion trace auf
unser Funktionsobjekt angewendet. Sie ist in Haskell-Syntax vereinfacht folgendermaßen definiert:
trace' :: ((p :*: a) -> (p :*: b)) -> (a -> b)
trace' f a = b where
(p :*: b) = f (p :*: a)
--
trace = mf trace'
Der Funktion f wird also ein Teil p ihres Rückgabewertes als Teil ihrer Argumente übergeben.
Das geht, weil Haskell
Lazy Evaluation
hat.
Danach muss das Ergebnis nur noch aus dem (()->)-Funktor ausgepackt werden, was in dieser Notation mittels unpack geht.
Die Spur, die wir auf diese Weise erhalten, ist einfach der Morphismus, der die Addition zweier Zahlen auf etwas umständliche Weise durchführt:
Das erste Argument dreht eine Extrarunde, bevor es zum zweiten addiert wird.
Da der Wert auf seinem Weg nach oben in der linken Wand des Funktorkastens versteckt ist, ist er vor unkontrollierter Löschung und Duplikation geschützt; duale Objekte werden nicht benötigt.
Kann man damit auch etwas sinnvolles anfangen? Ja, und zwar rekursive Funktionen definieren.
Das geht so: Man führt eine Leitung aus _ids, die später die rekursive Funktion als Wert führen wird, in den Funktorkasten
der Funktionsdefinition. Dann kann man dort die Funktion sich selbst aufrufen lassen (mit apply). Wenn man die eigentliche
Definition fertig hat, schließt man die Funktorbox und dupliziert die soeben definierte Funktion mit _dup.
Dann mache man noch einen Funktorkasten drumherum, um die Spur zu bekommen. Eines der beiden Duplikate der rekursiven Funktion wird also mittels
trace und param (oder (_const _id)) nach oben zurückgeführt,
damit es für seine eigene Definition zur Verfügung steht. Das andere Duplikat wird mittels
unpack aus dem Funktorkasten, der sich nach Anwendung von trace
ja nur noch auf den (()->)-Funktor bezieht, herausgeleitet.
Hier ist ein Beispiel, das die unendliche Liste aller natürlichen Zahlen berechnet:
test10 :: Num a => [a]
test10 = cnCurry $ unsingleton . dataFlow
( ( (_const _id) )
|> ( fd({------------------}_id{-----------------}) )
|> ( fd( _id ) )
|> ( fd( ({-------}packC{-----------}) ) )
|> ( fd( param<|fd( _id ) ) )
|> ( fd( fd( _id… _id ) ) )
|> ( fd( fd( _dup… _id ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _id… _id… _id… (_const 1) ) ) )
|> ( fd( fd( _id… _swap… _id ) ) )
|> ( fd( fd( _id… _id… _id… _id ) ) )
|> ( fd( fd( _id… _id… _plus ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _id… apply ) ) )
|> ( fd( fd( _id… _id ) ) )
|> ( fd( fd( _id… _id ) ) )
|> ( fd( fd( (mc2_1 (:)) ) ) )
|> ( fd( fd( _id ) ) )
|> ( fd( fd({------}_id{---------------------}) ) )
|> ( fd( _id ) )
|> ( fd( _dup ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( trace|>fd( _id ) )
|> ( fd( _id ) )
|> ( ({-----------------}unpack{-----------------}) )
|> ( _id )
|> ( _id… (_const 0) )
|> ( _id… _id )
|> ( apply )
|> ( _id )
)
Ein weiteres Beispiel für eine rekursive Funktion ist der Fixpunktkombinator. In normalem Haskell ist er so definiert:
fix :: (t -> t) -> t
fix f = f (fix f)
oder
fix f = x where x = f x
Er berechnet für eine gegebene Funktion einen Wert, der von dieser Funktion nicht verändert wird. Man kann den Fixpunktkombinator benutzen, um
rekursive Funktionen zu definieren, ohne dass die Funktionsdefinition syntaktisch gesehen rekursiv ist. Um die rekursive Funktion f::x->y
zu definieren, definiert man zunächst eine Funktion f'::r->x->y, indem man in der rekursiven Definition von f
jedes Vorkommen von f durch den ersten Parameter von f' ersetzt. Die Funktion f ist dann der Fixpunkt von
f', also (fix f'). So sieht der Fixpunktkombinator als Diagramm aus:
_fix :: DataFlow (DataFlow (a :*: ()) (a :*: ()) :*: ()) (a :*: ())
_fix = ( _id )
|> ( ({------}packC{-----}) )
|> ( param<|fd( _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _swap ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( apply ) )
|> ( fd( _id ) )
|> ( fd( _id ) )
|> ( fd( _dup ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( trace|>fd( _id ) )
|> ( fd( _id ) )
|> ( ({------}unpack{------}) )
|> ( _id )
|> ( _id )
Und so kann man ihn verwenden, um die Liste aller natürlichen Zahlen zu erzeugen:
test7 :: Num a => [a]
test7 = cnCurry $ unsingleton . dataFlow
( ( (_const _id) )
|> ( fd({------------------}_id{-----------------}) )
|> ( fd( _id ) )
|> ( fd( ({-------}packC{-----------}) ) )
|> ( fd( param<|fd( _id ) ) )
|> ( fd( fd( _id… _id ) ) )
|> ( fd( fd( _dup… _id ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _id… _id… _id… (_const 1) ) ) )
|> ( fd( fd( _id… _swap… _id ) ) )
|> ( fd( fd( _id… _id… _id… _id ) ) )
|> ( fd( fd( _id… _id… _plus ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd( _id… apply ) ) )
|> ( fd( fd( _id… _id ) ) )
|> ( fd( fd( _id… _id ) ) )
|> ( fd( fd( (mc2_1 (:)) ) ) )
|> ( fd( fd( _id ) ) )
|> ( fd( fd({------}_id{---------------------}) ) )
|> ( fd( _id ) )
|> ( fd({----------------}_id{-------------------}) )
|> ( _id )
|> ( _fix… (_const 0) )
|> ( _id… _id )
|> ( apply )
|> ( _id )
)
Wann kann man diesen Spurbildungsmechanismus für andere monoidale Kategorien C, die Spurbildung zulassen, verallgemeinern?
Allgemeinerweise ist die Spurbildung ja als Familie von Funktionen auf den Morphismen definiert, muss also selbst nicht unbedingt durch einen
Morphismus wie trace darstellbar sein.
Eine wichtige Voraussetzung dafür, dass das geht, ist, dass die Kategorie
abgeschlossen ist, das heißt im Wesentlichen,
dass die Typen von Morphismen wieder Objekte der Kategorie sind. Nur deswegen konnten wir oben einen Morphismus
m von (P × A) nach (P × B) in ein Objekt unter dem
(P × A →)-Funktor verpacken und von dem gefunktorten Objekt mittels trace die Spur ermitteln.
Es bedarf auch einer Möglichkeit, die Inputs (vom Typ A) für die Spur ins Innere des Funktorkastens zu leiten, wie ich es hier mit packC gemacht habe.
Dazu hat eine abgeschlossene Kategorie C ein Einheitsobjekt I
damit man einen packC-ähnlichen Morphismus vom Objekt A zum Objekt (I → A) bilden kann. Dieser Morphismus ist gegeben durch eine
natürliche Transformation vom Identitätsfunktor zum (I →)-Funktor, die umkehrbar sein sollte, damit man am Ende wieder einen
unpack-artigen Morphismus von (I → B) nach B anwenden kann, um so als Ergebnis der Spurbildung insgesamt einen Morphismus von A nach B zu bekommen.
Das Einheitsobjekt Objekt muss nicht mit dem neutralen Objekt des monoidalen Produkts identisch sein, zum Beispiel in der Kategorie der Kontrollflussgraphen
(siehe oben).
Wenn man ein Einheitsobjekt hat, kann man von Elementen eines Objekts O sprechen – diese sind gegeben durch die Morphismen von I nach O.
Und natürlich müssen in der Kategorie C Morphismen existieren, die die Rolle von param und trace übernehmen.
Alternativ zu Morphismen analog zu param, packC und unpack können in einer
abgeschlossenen monoidalen Kategorie
auch Morphismen analog zu (_const id) und apply verwendet werden, indem man zu Anfang einen Morphismus
vom monoidalen Identitätsobjekt zum Objekt ((P A) → (P A)) setzt, der den in ein Objekt verpackten
Identitätsmorphismus von (P A) erzeugt,
dann das Bild von m unter dem ((P A) →)-Funktor gefolgt von trace anwendet und schließlich den apply-Morphismus benutzt, um
den in ein Element von (A → B) verpackten Morphismus mit dem Identitätsmorphismus von A zu verbinden, der die ganze Zeit rechts daneben stand.
Das monoidale Produkt muss nicht unbedingt kartesisch sein, damit apply als Morphismus von ((A → B) A) nach B existieren kann;
in der Kategorie der Kontrollflussgraphen (mit der disjunkten Vereinigung als monoidalem Produkt) funktioniert das zwar nicht, aber in der Kategorie
der endlichdimensionalen Vektorräume und linearen Abbildungen mit den Tensorprodukt gibt es apply als lineare Abbildung von
(A* ⊗ B) ⊗ A nach B, die durch die entsprechende
Tensorkontraktion
gegeben ist.
Dass es mit Kontrollflussgraphen nicht geht, liegt daran, dass diese Kategorie zwar abgeschlossen und monoidal ist, die beiden Strukturen aber nicht miteinander
kompatibel sind, weil das Einheitsobjekt, dass für die Abgeschlossenheit benötigt wird, nicht dasselbe ist wie das Einheitsobjekt des monoidalen Produkts und weil
der (⊕ X)-Funktor nicht adjungiert zum (X →)-Funktor ist.
Trotzdem gibt es in der Kategorie der Kontrollflussgraphen eine Spurbildung, die dem Erzeugen von Schleifenkonstrukten entspricht.
Da die Morphismen hier Funktionen sind und alle Funktionstypen als Objekte der Kategorie vorkommen, sollte es auch möglich sein, Spurbildung
ähnlich wie in der Kategorie der Datenflussgraphen mit param und trace zu implementieren.
Die trace-Funktion muss deutlich anders definiert sein, hier gezeigt für einen
Morphismus beispielmorphismus, der die disjunkte Vereinigung dreier Datentypen auf die disjunkte Vereinigung von zwei Datentypen abbildet:
| |
. | |
(_const beispielmorphismus) | | |
| = (trace' beispielmorphismus)
trace |
| |
Hierbei ist . ein Morphismus, der einen Summanden zur disjunkten Vereinigung der Datentypen hinzufügt,
und trace' ist rekursiv definiert als
| | | | | |
(trace' morphismus) = morphismus
| | |
| | . . |
| | | | |
| (trace' morphismus) |
| | |
| \/
| |
Der Morphismus \/ bildet hierbei die disjunkte Vereinigung eines Datentyps T mit sich selbst auf den Typ T ab, indem er einfach vergisst,
aus welchem Summanden der Wert kam.
Die Morphismen . und \/ definieren übrigens zusammen ein
Monoid für jeden Typ T:
Der Morphismus . erzeugt ein neutrales Element, und \/ macht aus zwei Werten vom Typ T
auf assoziative Weise einen einzigen. Andere Monoide, in der Kategorie der Datenflussgraphen, die aber nur für Zahlen-Typen
definiert sind, wären _plus mit (_const 0)
und _mult mit (_const 1).
Bevor wir den Spur-Operator für die Kategorie der Kontrollflussgraphen in Aktion zu sehen, schauen wir erstmal genauer an, wie man in Haskell mit dieser Kategorie arbeiten kann.
Mit jedem _id-Draht ist ein Datentyp assoziiert. Von mehreren parallelen Drähten kann zur Ausführungszeit nur
jeweils nur einer Daten enthalten, da das Nebeneinanderschreiben ja der disjunkten Vereinigung der Datentypen entspricht.
Um etwas sinnvolles in dieser Kategorie ausdrücken zu können, müssen wir beschreiben können, was mit den Daten passieren soll.
Dazu eignen sich Datenflussgraphen besser. Wir brauchen also eine Möglichkeit, Datenflussgraphen in den Kontrollflussgraphen einzubetten.
Dafür eignet sich wieder ein Funktor, diesmal einer von der Kategorie der Datenflussgraphen in die Kategorie der Kontrollflussgraphen.
Ich habe den Funktor DFF genannt. Der Datentyp eines Paares von ganzen Zahlen in der Kategorie der Kontrollflussgraphen
wäre dann beispielsweise DFF (Int :*: Int :*: ()). Um Zugriff auf die Elemente in dem Paar zu haben, öffnet man einen
Funktorkasten und schreibt darin einen Datenflussgraphen.
Ein wichtiger Morphismus in der Kategorie der Kontrollflussgraphen ist der für Verzweigung des Kontrollflusses. Ich habe ihn _if
genannt.
Er erwartet als Input ein DFF-gefunktortes Tupel vom Typ DFF (Bool :*: rest) (für irgendeinen Tupeltyp rest)
und macht daraus ein Element der disjunkten Vereinigung von DFF rest mit sich selbst: Wenn das linkeste Element des Tupels den Wert
True hat, wird der restliche Teil der Daten (der mit dem Typ DFF rest) als dem linken Summanden der disjunkten Vereinigung
zugehörig markiert, ansonsten als dem rechten Summanden zugehörig.
Ein weiterer wichtiger Morphismus ist derjenige zum Zusammenfügen von Kontrollflüssen, den ich oben \/ und in Haskell _codup
(Coduplikation) genannt habe.
Hier ist ein Beispiel, das _if, _codup und den DFF-Funktor demonstriert:
collatzStep =
( ( _id )
|> ( _id::Typ ControlFlow (DFF(Integer:*:[Integer]:*:())) )
|> ( _id )
|> ( _id )
|> ( fd({-----------}_id…{-----------}_id ) )
|> ( fd( _id… _id ) )
|> ( fd( (_dup)… _id ) )
|> ( fd( _id… _id… _id ) )
|> ( fd( _id… (_dup)… _id ) )
|> ( fd( _id… _id… _id… _id ) )
|> ( fd( (_even)… _id… (mc2_1 (:))) )
|> ( fd( _id… _id… _id ) )
|> ( fd({-----}_id…{-----}_id…{------}_id ) )
|> ( _id )
|> ( _id )
|> ( _id )
|> ( (_if) )
|> ( _id… _id )
|> ( _id… _id )
|> ( _id… _id )
|> ( fd({---}_id…{--------}_id )… fd({---}_id…{-----------}_id ) )
|> ( fd( _id… _id )… fd( _id… _id ) )
|> ( fd( _id… (mc 2)… _id )… fd( _id… (mc 3)… _id ) )
|> ( fd( _id… _id… _id )… fd( _id… _id… _id ) )
|> ( fd( (_div)… _id )… fd( (_mult)… _id ) )
|> ( fd( _id… _id )… fd( _id… _id ) )
|> ( fd({----}_id…{-------}_id )… fd( _id… (mc 1)… _id ) )
|> ( _id… fd( _id… _id… _id ) )
|> ( _id… fd( _plus… _id ) )
|> ( _id… fd( _id… _id ) )
|> ( _id… fd({------}_id…{--------}_id ) )
|> ( _id… _id )
|> ( _id… _id )
|> ( (_codup) )
|> ( _id )
)
Der Input ist ein Paar, bestehend aus einer ganzen Zahl und einer Liste von ganzen Zahlen.
Im ersten Funktorkasten wird das erste Element des Paares verdreifacht. Die linkeste Kopie
wird getestet, ob sie eine gerade Zahl ist. Die rechteste Kopie wird an die Liste vorne angefügt.
Das Ergebnis ist ein Tripel, bestehend aus einem Wahrheitswert, der ganzen Zahl und der verlängerten Liste.
Dann wird der Funktorkasten geschlossen und das Tripel an den Morphismus _if übergeben. Je nachdem, ob der Wahrheitswert
True oder False war, wird danach der linke oder der rechte Teil des Folgenden ausgeführt.
Im linken Teil, also wenn sie gerade ist, wird die ganze Zahl durch 2 geteilt und im rechten Teil, also wenn sie ungerade ist,
wird sie mit 3 multipliziert und um 1 erhöht. Anschließend werden die beiden alternativen Kontrollflüsse wieder vereinigt.
Dieses Kontrollflussdiagramm berechnet also einen einzelnen Schritt zur Erzeugung einer
Collatz-Folge.
Wie sieht es mit der Berechnung der kompletten Sequenz für eine gegebene Zahl aus?
(Ich gehe hier mal davon aus, dass die Collatz-Vermutung zutrifft, sodass wir abbrechen können, sobald die 1 erreicht ist.)
Dazu müssen wir eine Schleife machen, und das geht mit param und trace. Hier ist der nötige Code:
collatz n = unsingleton . unDFF . fromLeft $ collatz' (Left (DFF (n:*:()))) where
fromLeft (Left a) = a
collatz' = controlFlow
( ( _id )
|> ( _id )
|> ( ({-------------}packC{--------------}) )
|> ( fd( _id ) )
|> ( fd( fd({---}_id{----------------}) ) )
|> ( fd( fd( _id ) ) )
|> ( fd( fd( _id… (mc []) ) ) )
|> ( fd( fd( _id… _id ) ) )
|> ( fd( fd({---}_id…{------}_id{----}) ) )
|> ( fd( _id ) )
|> ( param<|fd( _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _codup ) )
|> ( fd( _id ) )
|> ( fd( _id ) )
|> ( fd( (collatzStep) ) )
|> ( fd( _id ) )
|> ( fd( fd({-------------}_id…{------}_id ) ) )
|> ( fd( fd( _id… _id ) ) )
|> ( fd( fd( (mc 1)… _dup… _id ) ) )
|> ( fd( fd( _id… _id… _id… _id ) ) )
|> ( fd( fd( (mc2_1 (/=))… _id… _id ) ) )
|> ( fd( fd( _id… _id… _id ) ) )
|> ( fd( fd({-----}_id…{-----}_id…{---}_id ) ) )
|> ( fd( _id ) )
|> ( fd( _id ) )
|> ( fd( (_if) ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… _id ) )
|> ( fd( _id… fd( _id…{---}_id ) ) )
|> ( fd( _id… fd( _id… _id ) ) )
|> ( fd( _id… fd( (mc2_1 (:)) ) ) )
|> ( fd( _id… fd( _id ) ) )
|> ( fd( _id… fd( (mf reverse) ) ) )
|> ( trace|>fd( fd( _id ) ) )
|> ( fd( fd({----}_id{---}) ) )
|> ( fd( _id ) )
|> ( fd( _id ) )
|> ( ({-------------}unpack{-------------}) )
|> ( _id )
|> ( _id )
)
Eingabe ist ein DFF-gefunktortes 1-Tupel mit einer ganzen Zahl drin. Dieses wird mit packC
in den (()->)-Funktor eingepackt und anschließend um ein zweites Element – eine leere Liste – ergänzt.
Ich hätte auch erst die leere Liste hinzufügen können und es dann in den Funktor verpacken; es spielt keine Rolle.
Dann wird der Funktion ein Parameter hinzugefügt, wobei man bedenken muss, dass mehrparametrige Funktionen in der Kategorie der Kontrollflussgraphen
beim Aufruf immer nur ein einziges Argument übergeben bekommen, während die anderen Parameter leer bleiben. Welcher Parameter gefüllt
wird,
entscheidet darüber, wo in der Funktion mit mehreren Einsprungpunkten der Kontrollfluss beginnt.
Der Kontrollfluss hat jetzt zwei alternative Möglichkeiten: Entweder er kommt aus einem vorangegangenen Schleifendurchlauf (links) oder wir sind
gerade erst in die Schleife eingetreten (rechts). Da uns das für den bevorstehenden Schleifendurchlauf egal ist, werden die beiden Kontrollflüsse
mit _codup zusammengelegt. Anschließend wird ein einzelner Collatz-Schritt ausgeführt
(collatzStep, s.o.). Das Ergebnis ist wieder ein Paar aus einer
ganzen Zahl und einer Liste. Die ganze Zahl wird mit 1 verglichen, um die Abbruchbedingung zu prüfen.
Das spaltet den Kontrollfluss wieder in zwei Alternativen auf: Wenn die Zahl nicht 1 war,
springt er mittels trace an den Schleifenanfang zurück. Wenn sie dagegen 1 war, wird die Schleife verlassen.
Die 1 wird noch vorne an die Liste angehängt und die Liste umgedreht, um schöneren Output zu bekommen.
Danach (ich hätte es auch vorher machen können) wird die Liste aus dem (()->)-Funktor wieder ausgepackt.
Es ist ganz lustig, dass man ausführbare zweidimensionale Diagramme aus Haskell-Quellcode machen kann, aber auf Dauer etwas anstrengend, zumindest wenn die Diagramme gut aussehen sollen. Ein graphischer Editor wäre fein. Ich habe mal angefangen, einen solchen zu schreiben. Damit habe ich die beiden Bilder in diesem Artikel gemacht. Aber monoidale Funktoren und Monaden darstellen und ausführbaren Code erzeugen kann er noch nicht. Was auch noch schön wäre: Algebraische Manipulationen an den Morphismen und Funktoren einfach mit der Maus am Stringdiagramm vornehmen. Am Ende dieses Foliensatzes befindet sich ein Beispiel für einen Beweis, der auf der graphischen Manipulation von Stringdiagrammen beruht. Ein Programm, um solche graphischen Beweise zu erzeugen, könnte auch für Mathematik(didaktik)er interessant sein.
Es ist schwierig, dem Haskell-Typsystem beizubringen, wie es die Morphismen und Funktoren zusammensetzen soll. Manche Operationen konnte ich nicht in der Allgemeinheit definieren, in der ich es gern getan hätte. Vielleicht wäre es besser, eine eigens dafür konstruierte Sprache zu benutzen, deren Typsystem speziell auf monoidale Kategorien ausgelegt ist. Man könnte dann auch eine schönere Notation verwenden. Ich habe bereits Ideen, wie man man Typen selbst als Stringdiagramme darstellen kann.
Die Monaden-Operationen join
und pure
sind nur zwei Beispiele für
natürliche Transformationen.
Im Allgemeinen werden natürliche Transformationen in Stringdiagramm-Notation dargestellt als Knotenpunkte an den Seiten der
Funktorkästen, welche die Anzahl der Seitenwände und/oder die dazugehörigen Funktoren ändern. Damit besteht eine syntaktische
Ähnlichkeit zwischen natürlichen Transformationen und gewöhnlichen Morphismen: Beide haben Inputs und Outputs, nur dass es bei den Morphismen
Objekte sind und bei den natürlichen Transformationen Funktoren. Tatsächlich handelt es sich
bei natürlichen Transformationen um 2-Morphismen in der
2-Kategorie Cat, deren Objekte (gewöhnliche) 1-Kategorien
und deren 1-Morphismen Funktoren sind. Ähnlich wie Morphismen in einer monoidalen Kategorie kann man die 2-Morphismen einer 2-Kategorie
sowohl hintereinander als auch nebeneinander zusammensetzen. Der Unterschied ist, dass beim Nebeneinandersetzen auch die Quell-und Zielobjekte
der transformierten 1-Morphismen übereinstimmen müssen. Trotzdem haben 2-Kategorien ein ganz ähnliches Stringdiagramm-Kalkül wie monoidale Kategorien.
Und wenn man sich auf Endofunktoren beschränkt, also Funktoren von einer Kategorie in sich selbst,
stimmten die Quell- und Zielkategorien immer überein und man bekommt sogar eine monoidale Kategorie,
deren Objekte Endofunktoren sind und deren monoidales Produkt das Nebeneinandersetzen von natürlichen Transformationen ist.
In der Kategorie der Endofunktoren bilden die natürlichen Transformationen join
und pure
ein Monoid.
Ein Monoid in der Kategorie der Endofunktoren ist einfach eine Monade, was ist das Problem?
Jedenfalls wäre es interessant, wenn man in der Stringdiagramm-Notation diverse natürliche Transformationen zusammensetzen könnte.
Wie man das in Haskell umsetzen kann, weiß ich noch nicht. Ich habe es auch noch nicht probiert.
param und trace sind auch natürliche Transformationen oder besser die Komponenten davon,
und zwar in der Kategorie der Datenflussgraphen vom Funktor (T →) zum Funktor ((P × T) →)∘(P ×) beziehungsweise in der
anderen Richtung, und in der Kategorie der Kontrollflussgraphen
zwischen dem Funktor (T →) und dem Funktor ((P ⊕ T) →)∘(P ⊕). Wegen der Sonderrolle des monoidalen Produkts
(×) beziehungsweise (⊕) in diesen Kategorien sieht es dabei so aus, als würde auf der Innenseite des Funktorkastens an der natürlichen
Transformation ein Faktor vom Typ P eingeführt oder entfernt.
Diese Möglichkeit sollte also beim Design einer Stringdiagramm-Notation für natürliche Transformationen auch berücksichtigt werden.