Auf dieser Seite werden einige Modi meines Feldsimulationsprogrammes vorgestellt, die ich aus verschiedenen Gründen
nicht auf jene Seite packen wollte.
Sie basieren alle auf demselben Prinzip, das ich Wellengleichung mit Faserpotential
nenne und
zu dessen Erläuterung ich mathematisch etwas weiter ausholen werde.
Das Feld $\psi$ ist eine zeitabhängige vektorwertige Funktion (könnte man verallgemeinern zu einem Schnitt in einem Vektorbündel) auf einer Mannigfaltigkeit (Ich betrachte hier nur den flachen 2-Torus). Die Zeitentwicklung der $n$ Vektorkomponenten wird bestimmt durch die Gleichungen $$\frac{\text d^2 \psi_i}{\text d t^2} = \Laplace \psi_i - \frac{\text d V(\psi)}{\text d \psi_i},\quad 1\leq i\leq n.$$ Das ist die Wellengleichung zusammen mit einem Extra-Term, der den Einfluss einer potentiellen Energie $V$ darstellt. Die potentielle Energie hängt nur vom Wert von $\psi$ ab, nicht direkt vom Ort, ist also eine Funktion auf einem $n$-dimensionalen Raum.
Wenn man dem Feld $\psi$ wiederholt (kinetische) Energie entzieht (was man mit der Clear-Schaltfäche tun kann), wird es also versuchen, einen Zustand einzunehmen, der möglichst geringe potentielle Energie aufweist. Daher ist die Form der Menge der Minima von $V$ wichtig für das Verständnis der Phänomene, die auftreten können.
Im einem der einfachsten interessanten Fälle mit $n=2$ hat das Minimum die Form eines Kreises, auch genannt S¹. Der Graph des zugehörigen Potentials sieht dann zum Beispiel so aus:
Es wird Sombrero-Potential
genannt und durch die Formel
$$ V(\psi) = \left(\psi_1^2+\psi_2^2-1\right)^2$$
beschrieben.
In der graphischen Darstellung wird der Wert von $\psi$, der ja ein 2D-Vektor ist, durch Farbe kodiert.
Die Länge des Vektors bestimmt die Helligkeit und die Richtung des Vektors bestimmt den Bunttonwinkel.
Im folgenden Bild wird die Farbgebung zusammen mit dem Potential dargestellt:
Hier ist ein Beispielvideo für die Dynamik der Wellengleichung mit diesem Faserpotential:
Zu Anfang ist alles dunkel, weil $\psi$ mit relativ kleinen Werten initialisiert wird.
Doch dieser Zustand ist nicht stabil, und $\psi$ fällt
in das Potentialminimum;
da das Minimum allerdings nicht eindeutig ist, in einen von Ort zu Ort verschiedenen
Teil des Minimums. Daher sieht man helle Gebiete entstehen, die verschiedene Farben haben.
Die Wellengleichung sorgt dafür, dass es dabei glatt zugeht. Es gibt aber auch schwarze
Punkte. An diesen muss $\psi$ aus topologischen Gründen klein werden, denn wenn man eine
Schleife um einen solchen Punkt herum abläuft, und diese Bewegung mittels $\psi$ abbildet,
so läuft man einmal im kreisförmigen Potentialminimum entlang. Zieht man die Schleife im
Urbildraum auf einen Punkt zusammen, dann zieht sich auch die Schleife im Bildraum auf
einen Punkt zusammen. Dazu muss aber zwangsläufig irgendwann das Potentialminimum verlassen
werden. Das geschieht, um die Energie gering zu halten, nur in einer kleinen Region, die
dann als schwarzer Punkt erscheint.
Es gibt zwei Arten von stabilen schwarzen Punkten: Solche, die beim Umlaufen im Uhrzeigersinn
die Farben in der Reihenfolge rot-grün-blau ergeben, und solche, die rot-blau-grün ergeben.
Diese beiden Arten von topologischen Defekten mit entgegengesetzter Ladung
ziehen sich
gegenseitig an vernichten sich, sodass nur Wellen übrigbleiben. Wie Teilchen und Antiteilchen.
Aber es gibt auch eindimensionale Defekte, die Domänengrenzen heißen und daher kommen, dass $\psi$ auf der einen Seite der Domänengrenze in ein Minimum mit $\psi_3=\pi$ gefallen ist und auf der anderen Seite in ein Minimum mit $\psi_3=-\pi$. Die Punktdefekte sitzen aus energetischen Gründen besonders gern auf den Domänengrenzen, können sich aber auch wieder davon lösen.
Hauptsächlich, wenn sich eine Domänengrenze auf einen Punkt zusammenzieht, entsteht eine dritte Art von Phänomen: Blinkende, sich langsam fortbewegende Wellenpakete, sogenannte Breather-Solitonen. Ich vermute, dass sie aufgrund der Verwandtschaft zur Sine-Gordon-Gleichung zustandekommen. Die Breather-Solitonen können, wenn sie senkrecht genug auftreffen, eine Domänengrenze durchqueren.
Hier ist das Beispielvideo:
Man sieht an einigen Stellen einen großen schwarzen Punkt. Er entsteht durch eine lokale Veränderung des Potentials, die durch die Interaktion des Mauszeigers mit der Simulation hervorgerufen wird. Ich benutze ihn, um die Domänengrenzen herumzuziehen und Breather-Solitonen zu erzeugen. Man kann damit auch Punktdefekte ziehen.
Dieser Modus benutzt dieselbe Formel wie der vorige, aber ein anderes Farbschema, das die Punktdefekte besser zur Geltung bringt. Im Beispielvideo sieht man das seltene Phänomen, dass zwei Punktdefekte (die letzten beiden übrigen) sich nicht sofort annihilieren. Stattdessen geht aus der Kollision ein Punktepaar hervor, das sich kurze Zeit auseinanderbewegt, bevor es sich wieder vereinigt und endgültig in Wellen umwandelt.
Hier ist das Video:
In diesem Modus ist das Potential dreidimensional. Die Minima liegen auf drei paarweise orthogonalen Großkreisen der Einheitssphäre. Dadurch entstehen, wie ein aufgeblähtes Oktaeder, acht rechtwinklige gleichseitige sphärische Dreiecke. Diesen entsprechen acht verschiedene Arten von topologischen Defekten mit ihren Antidefekten. Um die Defekte zusätzlich zu verdeutlichen, wird in der Visualisierung die Helligkeit von Punkten reduziert, an denen ein hoher Wert des Potentials herrscht. Die Defekte sehen dreieckig aus.
Es gibt auch runde Defekte. Sie entsprechen einer Schleife um einen der Großkreise und entstehen durch Vereinigung von vier Defekten, die zu den vier sphärischen Dreiecken einer Hemisphäre gehören. Die runden Defekte zerfallen oft sofort wieder in vier dreieckige, die dann die zu den vier Dreiecken der anderen Hemisphäre gehörigen Antidefekte sind. Diese können sich dann wieder zu einem runden Defekt vereinigen, sodass es zu einer Oszillation zwischen den zwei Vierteilchenzuständen kommt. Man kann das daran erkennen, dass die Farbe zwischen den vier dreieckigen Defekten nach der Vereinigung und dem darauffolgenden Zerfall durch ihre Komplementärfarbe ersetzt wurde.
Im Beispielvideo kann man auch eine andere interessante Interaktion beobachten, in der sechs Dreiecksdefekte zu zwei Anti-Dreiecksdefekten reagieren. Wenn man nämlich eine Schleife um die sechs Defekte mit $\psi$ abbildet, bekommt man eine Schleife, die sechs sphärische Dreiecke umschließt. Das ist aber dasselbe wie wenn man die übrigen beiden Dreiecke im entgegengesetzten Sinn umläuft, was zwei Antidefekten entspricht. Daher können sich diese beiden Konfigurationen ineinander umwandeln.
Hier ist das Video:
Bei diesem Modus hat $\psi$ fünf Komponenten. Von den ersten beiden Komponenten hängt ein Sombreropotential ab, ebenso von den nächsten beiden. Die Sombreropotentiale werden additiv kombiniert, mit Gewichtungsfaktoren, die von der fünften Komponente abhängen: Bei negativen Werten der fünften Komponente ist das eine Potential stärker ausgeprägt und bei positiven Werten das andere. Dazu wird noch eine Funktion addiert, die Minima bei $\psi_5 = \pm \sqrt{10}$ hat, sodass die fünfte Komponente sich beim Betrag $\sqrt{10}$ mit verschiedenen Vorzeichen einpendelt. Es gibt also wieder Domänengrenzen.
Die genaue Formel ist: \begin{align} V(\psi)=&\frac 1{1+e^{-\psi_5}} \cdot \left(\psi_1^2+\psi_2^2-1\right)^2 \\ & + \left(1-\frac 1{1+e^{-\psi_5}}\right) \cdot \left(\psi_3^2+\psi_4^2-1\right)^2 \\ &+\frac 12 \left(\frac{\psi_5^2}{10}-1\right)^2 \end{align}
Die Defekte, die zum ersten Sombreropotential gehören, werden weiß dargestellt, die zum zweiten gehörigen schwarz. Die Größe der Defekte richtet sich nach der Ausprägung des zugehörigen Potentialterms: Je tiefer das Potential, desto kleiner ist der Kern des Defekts. In Domänen mit $\psi_5=-\sqrt{10}$ finden wir deshalb große weiße und kleine schwarze Defekte und in den anderen Domänen ist es andersrum.
Da die kleinen Defekte mehr potentielle Energie haben, wird Energie frei, wenn ein kleiner Defekt durch die Domänengrenze wandert und zu einem großen wird. Umgekehrt kostet es Energie, wenn ein großer Defekt in die andere Domäne überwechseln und dort zu einem kleinen werden soll. Daher kann eine wandernde Domänengrenze einen großen Defekt vor sich herschieben. Das kann man auch im Beispielvideo an der letzten übrigen Domänengrenze sehen:
Auch hier vernichtet sich das letzte Defektpaar nicht sofort.
In diesem Modus ist das Potential vierdimensional und gegeben als Summe von drei Sombreropotentialen.
Das erste Sombreropotential hängt von $\psi_1$ und $\psi_2$ ab $\left(\text{als } \left(\psi_1^2+\psi_2^2-1\right)^2\right)$ und hat seine Minima auf dem Zylinder mit der Gleichung $\psi_1^2+\psi_2^2=1$.
Das zweite Sombreropotential ist gegeben durch $\left(\psi_3^2+\psi_4^2-1\right)^2$ und hat seine Minima auf dem Zylinder mit der Gleichung $\psi_3^2+\psi_4^2=1$, der gegenüber dem ersten um $90^\circ$ isoklin verdreht ist. Die beiden Zylinder schneiden sich in einem skalierten Clifford-Torus.
Das dritte Sombreropotential ist gegeben durch $\frac 18\left(\left(\psi_1+\psi_3\right)^2+\left(\psi_2+\psi_4\right)^2-2\right)^2$. Es ist flacher als die ersten beiden und hat seine Minima auf einem Zylinder mit der Gleichung $\left(\psi_1+\psi_3\right)^2+\left(\psi_2+\psi_4\right)^2=2$. Dieser Zylinder ist mit den ersten beiden durch eine $45^\circ$-Drehstreckung verbunden und schneidet den Clifford-Torus in zwei Hopf-Kreisen.
Diese beiden Kreise sind die Minima des Gesamtpotentials. Da die Minima-Menge zwei nicht verbundene Komponenten hat, gibt es Domänengrenzen. Die beiden Arten von Domänen sind in der Visualisierung durch grünliche bzw. bläuliche Bereiche dargestellt. Punktdefekte, die einer Schleife um den ersten Zylinder entsprechen, sind rot eingefärbt und Punktdefekte, die zum zweiten Zylinder gehören, sind grün. Rote und grüne Defekte sitzen immer auf einer Domänengrenze, denn wenn man innerhalb des Clifford-Torus den einen Zylinder umläuft, ohne den anderen auch zu umlaufen, kommt man zwangsläufig in Bereiche, wo der dritte Summand des Potentials nicht 0 ist, und man schneidet beide Hopf-Kreise, läuft also durch beide Domänen. Diese Domänengrenze kann sich allerdings zu einem Punkt zusammenziehen. Dann überlagern sich der rote und der grüne Defekt zu einem gelben oder weißen Punkt, je nachdem ob die umgebende Domäne grünlich oder bläulich ist.
Aus irgendeinem Grund interagieren die gelben und weißen kombinierten Defekte mit Domänengrenzen, indem sie sich wieder in einen roten und einen grünen Defekt aufspalten, die dann nebeneinander auf der Domänengrenze sitzen.
Hier ist ein Beispielvideo:
Dieser Modus unterscheidet sich nur in der Startkonfiguration von dem vorherigen.
Am Anfang sind zwei rote und zwei grüne Defekte auf einen einzigen Punkt konzentriert, und an einem anderen Punkt sind die entsprechenden Antidefekte konzentriert. Diese beiden Vierfachdefekte sind jeweils von einer Domänengrenze umgeben. Da eine solche Doppelladung nicht stabil ist, spaltet sie sich in zwei gelbe Defekte auf, die jeweils aus einem roten und einem grünen Defekt bestehen. Die beiden gelben Defekte stoßen sich ab, bis sie irgendwann die Domänengrenze treffen. Dort spalten sie sich jeweils in einen roten und einen grünen Defekt auf und bleiben so auf der Grenze hängen. Die Domänengrenze zieht sich langsam zusammen, bis zwei gegenüberliegende Seiten der Domäne sich vernichten. Erst dann können die roten und grünen Defekte sich zu weißen zusammentun und sich weiter abstoßen.
Beispielvideo:
(mp4, webm, YouTube)
SO(3) ist die Menge aller Matrizen, die Drehungen des dreidimensionalen Raumes beschreiben. Es sind Orthonormalmatrizen, das heißt $M^\top M=\idMatrix_3$. Außerdem ist die Determinante 1. Das Potential mit der Gleichung $$ V(\psi) = \frob{M^\top M - \idMatrix_3}^2 + (\abs M - 1)^2, $$ wobei $\frob \cdot$ die Frobeniusnorm und $M$ eine Matrix ist, die die neun Komponenten von $\psi$ als Einträge hat, hat also als Minima die Elemente von SO(3).
Es gibt in SO(3) Schleifen, die sich nicht in SO(3) auf einen Punkt zusammenziehen lassen und die somit in der Wellengleichung mit jenem Faserpotential Punktdefekten entsprechen. Eine solche Schleife ist zum Beispiel eine Sequenz von Drehungen um irgendeine Achse, bei der der Winkel sich von $0$ bis $360^\circ$ ändert, wobei die SO(3)-Matrix für eine Drehung um $360^\circ$ die gleiche ist wie für eine Drehung um $0^\circ$; die Schleife schließt sich also. Man mache sich klar, dass man eine solche Sequenz nicht kontinuierlich zu einer konstanten Sequenz deformieren kann, die Schleife also nicht auf einen Punkt zusammenziehen kann. Allerdings kann man sie deformieren zu einer Sequenz, die andersherum dreht, also von $0^\circ$ bis $-360^\circ$. Das sieht man am einfachsten, wenn man sich SO(3) als Ball vorstellt, bei dem gegenüberliegende Punkte des Randes miteinander identifiziert werden. Ein Punkt $P$ in diesem Ball entspricht einer Drehung: Die Richtung vom Mittelpunkt nach $P$ ist die Drehachse und der Abstand vom Mittelpunkt entspricht dem Drehwinkel, so dass am Rand die $180^\circ$-Drehungen liegen. Die eben beschriebene Schleife von Drehungen ist dann eine orientierte Durchmesser-Strecke des Balls, und man kann sie in eine entgegengesetzt orientierte Schleife deformieren, indem man sie einfach um $180^\circ$ um eine zu ihr senkrechte Achse des Balles dreht.
Dass man den Umlaufsinn einer Schleife einfach umkehren kann, bedeutet, dass die zugehörigen Defekte ihre eigenen Antiteilchen sind. Es gibt hier also,
anders als bei Faserpotential / S¹
, nur eine einzige Art von Defekt, und jeder zieht jeden an und kann sich mit jedem annihilieren.
Mir ist leider kein Weg eingefallen, das überzeugend zu visualisieren. Die Visualisierung zeigt im Grünkanal den Wert des Potentials, im Rotkanal
die Spannungsenergie
von $\psi$ und im Blaukanal die kinetische Energie.
Hier ist ein Beispielvideo:
In diesem Modus ist das Potential 18-dimensional, entsprechend zwei 3×3-Matrizen $N$ und $M$.
Die Formel ist:
\begin{alignat}{3}
V &&= &&& \lambda_m\cdot\left(\frob{M^\top M - \idMatrix_3}^2 + (\abs M - 1)^2 \\
+ \frob{N^\top N - \idMatrix_3}^2 + (\abs N - 1)^2\right) \\
&&&&+ & \lambda_r\cdot\frob{M^\top M - \idMatrix_3}^2\cdot\frob{N^\top N - \idMatrix_3}^2 \\
&&&&+ & \lambda_c\cdot\frob{M^\top N - \idMatrix_3}^2
\end{alignat}
Von den ersten neun Dimensionen und von den letzten neun Dimensionen hängt jeweils ein Potential wie bei Faserpotential / SO(3)
ab, gewichtet mit
$\lambda_m=1$. Dies bewirkt zwei Arten von Defekten, die jeweils ihre eigenen Antiteilchen sind.
Dazu kommt ein Term, der verhindert, dass beide Matrizen gleichzeitig nicht orthonormal sind. Dieser Term ist mit $\lambda_r=10$ gewichtet und sorgt dafür, das die beiden verschiedenen Defekt-Arten nicht am selben Ort existieren können.
Schließlich erhöht der mit $\lambda_c=\frac 1{20}$ gewichtete Term die potentielle Energie, wenn die (nahezu orthonormalen) Matrizen $M$ und $N$ ungleich sind. Eine Schleife um einen einzelnen Defekt muss deswegen zwangsläufig Gebiete durchlaufen, wo dieser Term relativ groß ist. Nur wenn die Schleife sowohl um einen $M$-Defekt als auch um einen $N$-Defekt läuft, kann jeder Punkt der Schleife verschwindende potentielle Energie haben. Das bewirkt, dass sich zwischen zwei ungleichartigen Defekten eine bandförmige Region mit erhöhter Energie befindet, die bestrebt ist, sich möglichst klein zusammenzuziehen. Wegen des $\lambda_r$-Terms können die Defekte am Ende des Bandes nicht völlig zur Deckung kommen. Also finden sie sich zu eng beieinanderliegenden Pärchen zusammen.
Die Visualisierung stellt die Defekte rot bzw. grün dar und die Potentialenergie blau.
Hier ist ein Beispielvideo:
Diese Confinement
-Idee lässt sich auf Defekte übertragen, die von Sombreropotentialen verursacht werden.
Zunächst betrachten wir drei Arten von Defekten mit ihren Antidefekten, also ein sechsdimensionales Potential.
Um die Beschreibung zu vereinfachen, fasse ich jeweils zwei Komponenten von $\psi$ zu einer komplexen Zahl zusammen.
Da die Kerne der Defekte später durch rote, grüne bzw. blaue Farbe visualisiert werden, nenne ich die komplexen Zahlen
$\psi_r$, $\psi_g$ und $\psi_b$ und definiere sie als
\begin{align}
\psi_r &= \psi_1 + i\cdot \psi_2 \\
\psi_g &= \psi_3 + i\cdot \psi_4 \\
\psi_b &= \psi_5 + i\cdot \psi_6.
\end{align}
Ein Sombreropotential lässt sich dann mit der Definition
$$ m(z)= \left(\abs z^2 - 1 \right)^2$$
kompakt schreiben.
Wenn man will, dass zwischen einzelnen Defekten verschiedener Art wie oben Bänder aus erhöhter Energie existieren, die sie zu Gruppen zusammenziehen, muss man die Potentialenergie erhöhen, wenn die Winkel innerhalb der Minimumskreise der Sombreropotentiale ungleich sind. Wegen der Sombreropotentiale darf man davon ausgehen, dass abgesehen von den Kernen der Defekte die komplexen Zahlen überall ungefähr den Betrag 1 haben. Daher kann man einfach einen Term der Form $\Re\left(1-\psi_{r}\overline{\psi_{g}}\right)\ \left(\approx 1 - \cos \left(\arg{\psi_r}-\arg{\psi_g}\right)\right)$ benutzen, damit sich die $\psi_r$-Defekte und die $\psi_g$-Defekte anziehen.
Die vollständige Potentialgleichung, bei der sich die Defekte zu Dreiergruppen zusammenfinden, aber auf kurze Distanz abstoßen, lautet: \begin{alignat}{3} V(\psi)&& = &&& \lambda_m\cdot\left( m(\psi_{r})+m(\psi_{g})+m(\psi_{b})) \right) \\ &&&&+ & \lambda_r\cdot\left(\left((m(\psi_{r})+m(\psi_{g})+m(\psi_{b})\right)^2 \\ - \left(m(\psi_{r})^2+m(\psi_{g})^2+m(\psi_{b})^2\right) \right) \\ &&&&+ & \lambda_c\cdot\left( \Re\left(1-\psi_{r}\overline{\psi_{g}}\right) +\Re\left(1-\psi_{g}\overline{\psi_{b}}\right) +\Re\left(1-\psi_{b}\overline{\psi_{r}}\right) \right) \end{alignat} mit $\lambda_m=1$, $\lambda_r=3$ und $\lambda_c=\frac 1{10}$.
Hier ist ein Beispielvideo:
Disclaimer: Echte Quarks funktionieren ganz anders.
Hier gibt es wie eben drei Farben, aber von jeder gibt es eine helle und eine dunkle Variante.
Das Potential ist also zwölfdimensional, und der $\lambda_m$-Term setzt sich aus sechs Sombreropotentialen zusammen.
Die zugehörigen komplexen Zahlen nenne ich $\psi_{ru}, \psi_{gu}, \psi_{bu}$ für die hellen Farben ($u$ für up
)
und $\psi_{rd}, \psi_{gd}, \psi_{bd}$ für die dunklen Farben ($d$ für down
).
Für das Confinement zählt jeweils nur die Summe der beiden Winkel gleicher Farbe, also das Produkt der komplexen Zahlen. Zum Beispiel lautet der Term für die Anziehung von roten und grünen Defekten $$\Re\left(1-\psi_{ru}\psi_{rd}\overline{\psi_{gu}\psi_{gd}}\right).$$
Dadurch finden sich wieder je drei Defekte mit unterschiedlichem Farbton zu Gruppen zusammen, wobei die Helligkeit egal ist.
Es ist aber auch möglich, dass sich ein Defekt und ein Antidefekt mit demselben Farbton, aber unterschiedlicher Helligkeit, zu einem
Meson
zusammentun, da auf einer Schleife um so ein Gebilde ebenfalls die Confinement-Energie verschwinden kann.
Hier ist ein Beispielvideo:
Dieser Modus funktioniert fast so wie Faserpotential / Quarks / Confinement
, nur dass die $\lambda$-Gewichtungsfaktoren anders sind
und $\psi_r$ sowie $\psi_g$ in den Confinement-Termen quadriert statt einfach vorkommen. Letzteres hat zwei Auswirkungen:
Erstens bilden sich netzartige Strukturen aus Confinement-Energie (hier zur Abwechslung schwarz dargestellt), in denen die Punktdefekte eingebettet sind.
Zweitens besteht die minimale isolierte Struktur, also das kleinste Gebilde aus Defekten, um das man eine Schleife mit verschwindender potentieller Energie
legen kann, aus einem roten, einem grünen und zwei blauen Defekten.
Die beiden blauen Defekte stoßen sich ab, werden aber durch das Confinement an die beiden anderen Defekte gebunden.
Dadurch entsteht ein langgestrecktes Molekül
. Hier ist eine Momentaufnahme von einem Molekül und einem Antimolekül aus dem Beispielvideo:
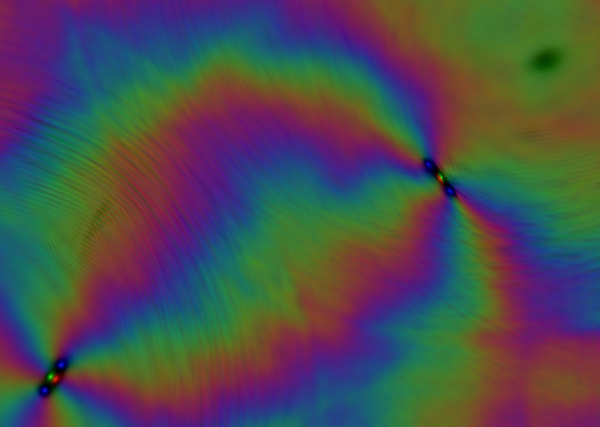
Der dunkle Fleck oben rechts ist übrigens ein wanderndes Breather-Soliton, wohl wieder aufgrund der Verwandtschaft zur Sine-Gordon-Gleichung. In diesem Fall ist die Verwandtschaft aber nicht so offensichtlich.
Die Formel für das Potential lautet: \begin{alignat}{3} V(\psi)&& = &&& \lambda_m\cdot\left( m(\psi_{r})+m(\psi_{g})+m(\psi_{b})) \right) \\ &&&&+ & \lambda_r\cdot\left(\left((m(\psi_{r})+m(\psi_{g})+m(\psi_{b})\right)^2 \\ - \left(m(\psi_{r})^2+m(\psi_{g})^2+m(\psi_{b})^2\right) \right) \\ &&&&+ & \lambda_c\cdot\left( \Re\left(1-\psi_{r}^2\overline{\psi_{g}^2}\right) +\Re\left(1-\psi_{g}^2\overline{\psi_{b}}\right) +\Re\left(1-\psi_{b}\overline{\psi_{r}^2}\right) \right) \end{alignat} mit $\lambda_m=1$, $\lambda_r=1$ und $\lambda_c=\frac 16$.
Hier ist das Beispielvideo: