Inside an otherwise empty universe with Newtonian physics there is a spaceship. The spaceship is spherical and built so symmetrically that the center of mass coincides with the center of the sphere. On the equator of the sphere there is an array of thruster jets arranged in such a way that during acceleration the effective point of application of the thrusting forces agrees with the center of mass; thus there cannot be any torques. In the center of the spaceship, one end of the axis of a spinning gyroscope is mounted in a frictionless manner; the other end floats freely and points towards the equator. The gyroscope was not considered when determining the center of mass of the spaceship. Due to the frictionless suspension in the center of mass of the spaceship, motions of the gyroscope, though they may translate the spaceship by means of reaction forces, cannot exert any torque.
Here's a sketch:
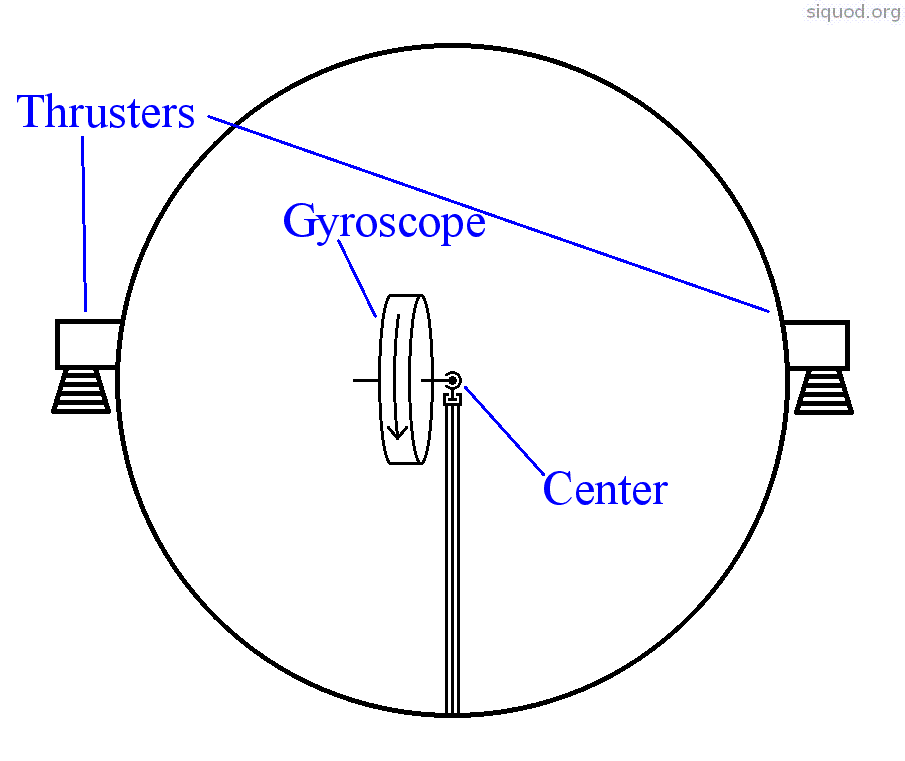
Now the spaceship accelerates. In the beginning, the gyroscope has an angular momentum L, but due to the acceleration forces it starts precessing and after a while it has the angular momentum -L. That's when the spaceship stops accelerating. Angular momentum must be conserved. Where have the 2L difference in angular momentum gone?